Trong bài học hôm nay, các bạn học sinh hãy cùng Tiếng Anh trẻ em BingGo Leaders tìm hiểu về hình thoi cũng như cách tính diện tích hình thoi để dễ dàng chinh phục các bài tập hay bài kiểm tra trên lớp nhé!
1. Hình thoi là gì?
1.1. Khái niệm hình thoi
Hình thoi trong hình học Ơ-clít là một loại tứ giác có đặc điểm chính là bốn cạnh đều. Chính xác hơn, đây là một hình bình hành, trong đó hai cạnh kề bằng nhau và hai đường chéo vuông góc với nhau.
Khi một hình thoi có 4 góc vuông bằng nhau thì hình thoi đó được xác định là một hình vuông. Từ đây ta có thể suy ra hình vuông là một trường hợp đặc biệt của hình thoi vì nó có 4 cạnh dài bằng nhau và có 4 góc vuông.
Từ kiến thức trên ta có thể rút ra kết luận
- Tất cả hình vuông đều là hình thoi, nhưng mọi hình thoi thì không phải đều là hình vuông
- Mọi hình thoi đều là hình bình hành, nhưng mọi hình bình hành thì không phải hình thoi.
1.2. Dấu hiệu nhận biết
Tính diện tích hình thoi là 1 trong những kiến thức quan trọng mà các em học sinh sẽ được học ở chương trình toán lớp 4. Để nhận biết hình thoi, chúng ta có thể dựa vào các dấu hiệu sau đây:
- Tứ giác có bốn cạnh bằng nhau là hình thoi.
- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
- Hình bình hành có hai đường chéo là đường phân giác của một góc là hình thoi.
Học sinh sẽ được học chi tiết hơn về các dấu hiệu này ở toán học cấp 2. Còn riêng ở cấp 1, các em chỉ cần nắm vững định nghĩa về hình thoi và cách vẽ hình thoi đúng.
1.3. Tính chất hình thoi
Một hình thoi thường có những tính chất sau:
- Các cạnh đối song song với nhau
- Các góc đối nhau bằng nhau.
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc của hình thoi.
- Hình thoi có tất cả tính chất của hình bình hành.
2. Công thức tính diện tích hình thoi
2.1 Công thức tính diện tích hình thoi dựa vào đường chéo
Diện tích của hình thoi được tính bằng một nửa tích độ dài của hai đường chéo. Đường chéo của hình thoi là đường thẳng nối hai đỉnh đối diện với nhau. Hai đường chéo này vuông góc với nhau và cắt nhau tại một điểm.
Công thức tính diện tích hình thoi:
|
S = 1/2 x (d1 x d2) |
|
Trong đó:
|

Cách tính diện tích hình thoi dựa vào đường chéo
Để tính diện tích của hình thoi dựa vào đường chéo, ta tiến hành theo từng bước dưới đây:
- Bước 1: Xác định độ dài, kích thước của hai đường chéo hình thoi
- Bước 2: Nhân độ dài hai đường chéo với nhau.
- Bước 3: Chia tích của hai đường chéo cho 2 và ta sẽ được kết quả là diện tích hình thoi.
Ví dụ:
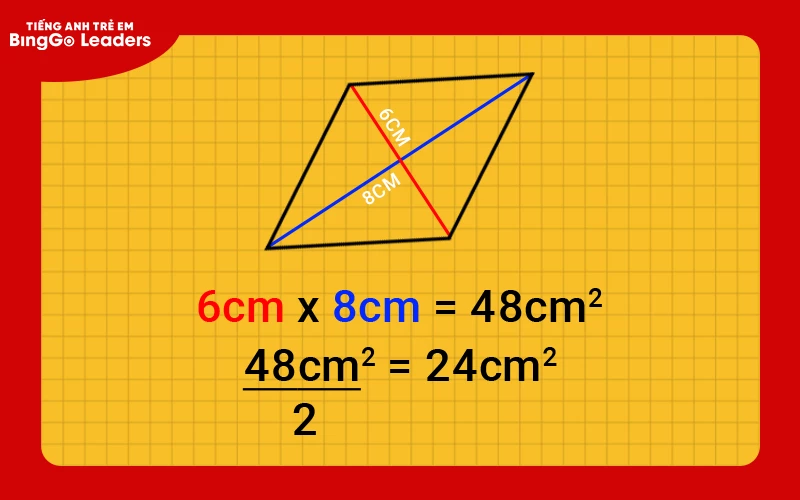
Ta có độ dài 2 đường chéo hình thoi là 6 cm và 8 cm.
Trong ví dụ trên, ta có tích 2 đường chéo = 6 cm x 8 cm = 48 cm2 (Lưu ý đơn vị của diện tích phải là bình phương)
Áp dụng công thức tính diện tích hình thoi bằng 1 nửa tích của 2 đường chéo ta có:
S = 1/2 x 48 = 24 cm2
Vậy là diện tích hình thoi = 24 cm2
Xem thêm: CÁCH TÍNH CHU VI HÌNH TAM GIÁC KÈM VÍ DỤ VÀ BÀI TẬP ỨNG DỤNG
2.2 Công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
Ngoài cách sử dụng đường chéo, học sinh có thể sử dụng cách tính diện tích hình thoi bằng cách sử dụng cạnh đáy và chiều cao của nó:
|
S = h x a |
|
Trong đó:
|

Cách tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
Để tính diện tích hình thoi dựa trên chiều cao và cạnh đáy, ta thực hiện theo quy trình sau:
- Bước 1: Xác định số đo chiều cao và cạnh đáy của hình thoi.
- Bước 2: Nhân số đo chiều cao với số đo cạnh đáy của hình thoi.
Ví dụ:
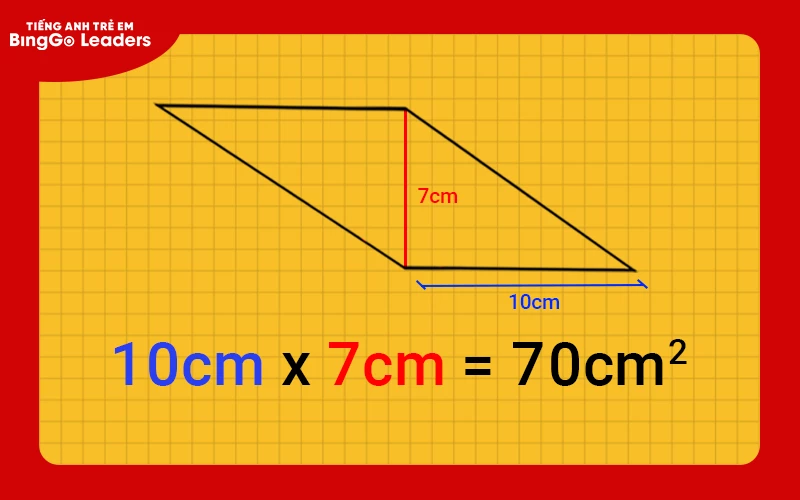
Chúng ta có chiều cao của hình thoi là 7 cm và đáy là 10 cm
Áp dụng công thức tính diện tích hình thoi dựa theo cạnh đáy và chiều cao, bạn hãy nhân chúng lại với nhau để có được diện tích hình thoi.
Ta có: 10 cm x 7 cm = 70 cm2
Vậy là diện tích hình thoi = 70 cm2
Xem thêm: [HƯỚNG DẪN] cách tính diện tích hình tam giác lớp 5 chi tiết
2.3 Tính diện tích hình thoi dựa vào hệ thức trong tam giác
|
S= a². sin α. |
|
Trong đó:
|

Cách tính diện tích hình thoi dựa vào hệ thức trong tam giác
Các bước tính diện tích hình thoi dựa vào hệ thức trong tam giác như sau:
- Bước 1: Xác định độ dài của cạnh và số đo 1 góc bất kỳ thuộc hình thoi
- Bước 2: Bình phương độ dài cạnh bên
- Bước 3: Tính sin của góc đã xác định trong hình thoi
- Bước 4: Nhân kết quả đã tìm được ở bước 2 và bước 3
Ví dụ:
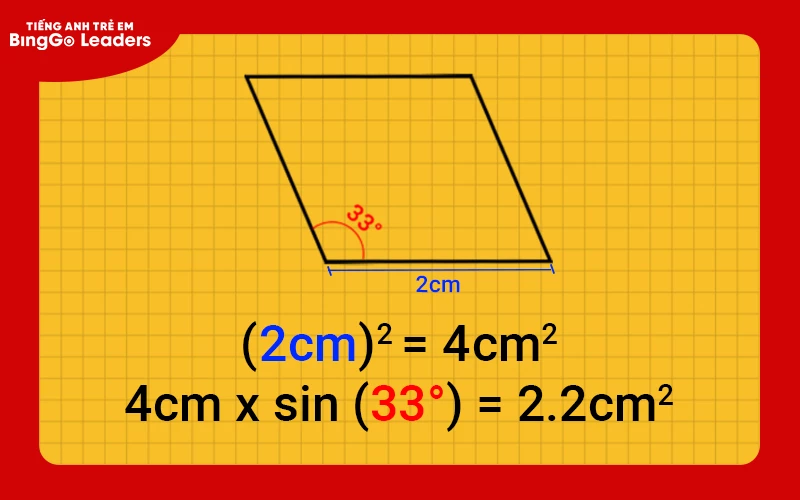
Cho hình thoi ABCD, có cạnh hình thoi = 2cm, góc A = 33 độ. Tính diện tích hình thoi ABCD.
Hình thoi ABCD có cạnh dài 2 cm => 2 cm x 2 cm = 4 cm2
Sau đó, chúng ta sẽ nhân giá trị vừa tính được với giá trị sin của góc A (33 độ)
Ta có: 4 cm2 x sin (33) = 2.2 cm2
Vậy là diện tích hình thoi ABCD = 2.2 cm2
Xem thêm: Thuộc lòng công thức tính chu vi hình bình hành kèm bài tập áp dụng
3. Một số bài tập ôn luyện cách tính diện tích hình thoi

Một số bài tập thực hành tính diện tích hình thoi
Bài tập 1: Tính diện tích hình thoi biết độ dài 2 đường chéo lần lượt là: AC = 50 cm, BD = 80 cm.
Lời giải:
Áp dụng công thức tính diện tích hình thoi bằng 1 nửa tích của 2 đường chéo AC và BD chúng ta có:
S = 1/2 (ACxBD) = 1/2 x (50 x 80) = 2000 cm2
Vậy diện tích hình thoi ABCD là 2000 cm2
Bài tập 2: Hãy tính diện tích hình thoi có đường chéo dài 153cm và đường chéo ngắn bằng 2/3 đường chéo dài.
Lời giải:
Độ dài đường chéo ngắn là
153 x 2/3 = 102 (cm)
Diện tích hình thoi là
1/2 x (153 x 102) = 7803 (cm2)
Vậy diện tích hình thoi là 7803 cm2
Bài tập 3: Cho hình thoi ABCD, có cạnh hình thoi = 4cm, góc A = 35 độ. Tính diện tích hình thoi ABCD.
Lời giải:
Áp dụng công thức, ta có a = 4, góc = 35 độ. Ta thay vào công thức như sau:
S = a2 x sinA = 42 x sin(35o) = 9,177 (cm2).
Vậy diện tích hình thoi ABCD là 9,177 cm2
Bài tập 4: Hãy tính diện tích hình thoi ABCD, biết độ dài 2 đường chéo lần lượt là 9cm và 12cm.
Lời giải:
Diện tích hình thoi ABCD là:
1/2 x (12 x 9) = 54 (cm2)
Vậy diện tích hình thoi là 54 cm2
Bài tập 5: Cho hình thoi ABCD, có cạnh AB = BC = CD = DA = 4cm, chiều cao hình thoi bằng 3cm. Hãy tính diện tích hình thoi.
Lời giải:
Áp dụng theo công thức diện tích hình thoi theo chiều cao và cạnh đáy, ta có h = 3cm, a = 4cm:
S = a x h = 3 x 4 = 12 (cm2).
Vậy diện tích hình thoi ABCD là 12 cm2
Bài tập 6: Cho hình thoi đo có độ dài hai đường chéo lần lượt là 7cm và 9cm. Hỏi diện tích của hình thoi đó bằng bao nhiêu?
Lời giải:
Áp dụng theo cách tính diện tích hình thoi, ta có d1 = 7cm và d2 = 9cm. Ta đưa vào công thức và có kết quả như sau:
S = 1/2 x (7 x 9) = 1/2 x 63 = 31,5 (cm2).
Vậy diện tích hình thoi ABCD là 31,5 cm2
Bài tập 7: Một hình thoi có tổng độ dài hai đường chéo là 423m, đường chéo thứ nhất gấp đôi đường chéo thứ hai. Tính diện tích hình thoi
Coi độ dài đường chéo thứ hai là 1 phần thì độ dài đường chéo thứ nhất là 2 phần
Lời giải:
Tổng số phần bằng nhau là: 1 + 2 = 3 (phần)
Độ dài đường chéo thứ nhất là: 423 : 3 x 1 = 141 (m)
Độ dài đường chéo thứ hai là: 423 - 141 = 282 (m)
Diện tích của hình thoi là: 1/2 x (141 x 282) = 19881 (m²)
Vậy diện tích hình thoi là 19881 m²
Bài tập 8: Hình thoi A có độ dài hai đường chéo gấp đôi độ dài hai đường chéo của hình thoi B. Hỏi hình thoi A có diện tích gấp mấy lần diện tích hình thoi B?
Lời giải:
Gọi độ dài hai đường chéo của hình thoi B lần lượt là a và b
Thì độ dài hai đường chéo của hình thoi A lần lượt là 2 x a và 2 x b
Diện tích của hình thoi B là: a x b : 2
Diện tích của hình thoi A là: 2 x a x 2 x b : 2 = 4 x a x b : 2
Vậy diện tích của hình thoi A gấp 4 lần diện tích của hình thoi B
Bài tập 9: Một hình thoi có diện tích 4dm, độ dài một đường chéo là 3/5dm. Tính độ dài đường chéo thứ hai.
Lời giải:
Độ dài đường chéo thứ hai là:
(4x2): 3/5 = 40/3 (dm)
Vậy độ dài đường chéo thứ hai là 40/3 dm
Bài tập 10: Tính diện tích hình thoi, biết:
- a) Độ dài các đường chéo là 1dm và 20 cm;
- b) Độ dài các đường chéo là 4 m và 12 dm.
Lời giải:
Gọi d1 và d2 lần lượt là độ dài của 2 đường chéo
- a) 1 dm và 20 cm
Đổi đơn vị: d1 = 1 dm = 10 cm, d2 = 20 cm
Diện tích của hình thoi là 1/2 x (10 x 20) = 100 (cm2)
- b) 4 m và 12 dm
Đổi đơn vị: d1 = 4 m = 400 cm, 12 dm = 120 cm
Diện tích của hình thoi là 1/2 x (400 x 120) = 24000 (cm2)
Xem thêm: TUYỂN TẬP TRUYỆN TIẾNG ANH CHO BÉ THIẾU NHI SONG NGỮ BA MẸ NÊN KỂ
4. Tìm hiểu thêm cách tính chu vi hình thoi
Chu vi hình thoi được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích.
Để tính chu vi hình thoi, ta tính tổng độ dài của 4 cạnh. Công thức cụ thể như sau:
|
P= a x 4 |
|
Trong đó:
|
Ví dụ: Cho một hình thoi ABCD có độ dài các cạnh bằng nhau và bằng 5 cm. Hỏi chu vi của hình thoi này bằng bao nhiêu?
Theo công thức tính chu vi hình thoi được giới thiệu ở trên, ta có a = 5 cm. Như vậy chu vi hình thoi ABCD sẽ được tính như sau:
P (ABCD) = a x 4 = 5 x 4 = 20 cm

Công thức tính chu vi hình thoi
5. Kết luận
Trên đây là những kiến thức cơ bản về cách tính diện tích hình thoi. Mong rằng những chia sẻ trên sẽ giúp phụ huynh và học sinh chinh phục các dạng toán tính diện tích hình thoi dễ dàng hơn. Cảm ơn các em học sinh đã đón đọc bài viết của Tiếng Anh trẻ em BingGo Leaders.
Xem thêm: LUYỆN VIẾT TIẾNG ANH CHO TRẺ TIỂU HỌC VỪA HIỆU QUẢ MÀ LẠI VUI VẺ








![[ÔN TẬP] CÁCH NHÂN MỘT SỐ VỚI MỘT TỔNG - TOÁN LỚP 4](/storage//images/2023/04/28/am-dem-trong-tieng-viet-18.webp)






