[HƯỚNG DẪN] CÁCH TÍNH DIỆN TÍCH HÌNH TAM GIÁC LỚP 5 CHI TIẾT

Vào cấp 2, bé sẽ được học sâu hơn về hình học. Vì vậy, ngay từ cuối cấp 1, giáo viên và phụ huynh cần trang bị cho bé những kiến thức căn bản về hình học như cách tính diện hình tam giác lớp 5 để bé khỏi bỡ ngỡ khi học về toán hình. 

BingGo Leaders đã tổng hợp những cách tính diện tích hình tam giác đơn giản, dễ hiểu qua bài viết dưới đây. Cùng tham khảo ngay nhé!

1. Nắm chắc kiến thức cơ bản về các hình tam giác

Việc nắm vững những kiến thức về hình tam giác sẽ giúp bé hiểu được nguồn gốc của công thức tính diện tích, hiểu rõ các quy tắc khi làm các bài tập. Vì vậy, trước khi dạy cho bé cách tính diện tích hình tam giác lớp 5 thì nên dạy cho bé hiểu rõ hình tam giác là gì, có mấy loại hình tam giác.

1.1. Hình tam giác là gì?

Tam giác là một hình phẳng, có 3 đỉnh không thẳng hàng với nhau và 3 cạnh là 3 đoạn thẳng nối từ 3 đỉnh. Tam giác là hình đa giác có số cạnh ít nhất, tổng các góc trong hình tam giác luôn bằng 180 độ.

Ở cấp độ kiến thức hình học lớp 5, bé chưa cần học quá nhiều về những tính chất của hình tam giác. Bé chỉ cần nắm rõ khái niệm hình tam giác là gì, có gì đặc biệt so với các hình khác. 

1.2. Phân loại các hình tam giác

Có nhiều loại hình tam giác, việc nắm rõ đặc điểm của từng hình sẽ giúp bé áp dụng công thức tính diện tích chuẩn và ra kết quả nhanh hơn. Thông thường, tam giác được phân thành 6 loại:

Phân loại tam giác theo độ dài các cạnh, gồm có: tam giác thường, tam giác cân, tam giác đều.

Phân loại tam giác theo số đo các góc, gồm có: tam giác vuông, tam giác vuông cân, tam giác tù.

2. Công thức tính diện tích hình tam giác lớp 5

Tùy vào từng loại hình tam giác mà sẽ có công thức tính diện tích khác nhau. Về cơ bản, ở cấp độ kiến thức lớp 5, bé cần nắm vững các cách tính diện tích hình tam giác sau đây:

2.1 Cách tính diện tích hình tam giác thường

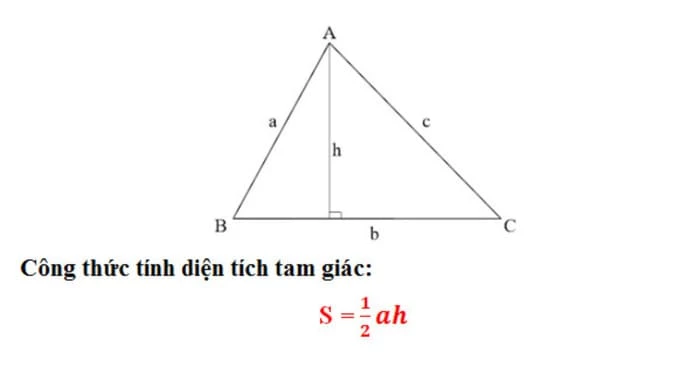
Đối với tam giác thường ABC có 3 cạnh a, b, c và đường cao h. Ta có công thức: 

S = (a x h)/2

Trong đó: 

• a là độ dài cạnh 
• h là độ dài đường cao  ( đoạn thẳng hạ từ đỉnh xuống đáy )

Như vậy, diện tích tam giác thường sẽ bằng ½ tích của đường cao hạ từ đỉnh và cạnh đối diện đỉnh đó.

Bài tập ứng dụng:

Tính diện tích hình tam giác ABC có độ dài đáy là 5m và chiều cao là 2,4m.

Giải:  Diện tích của hình tam giác ABC là: S=(5 x 2.4) : 2 = 6m2

2.2. Cách tính diện tích hình tam giác cân

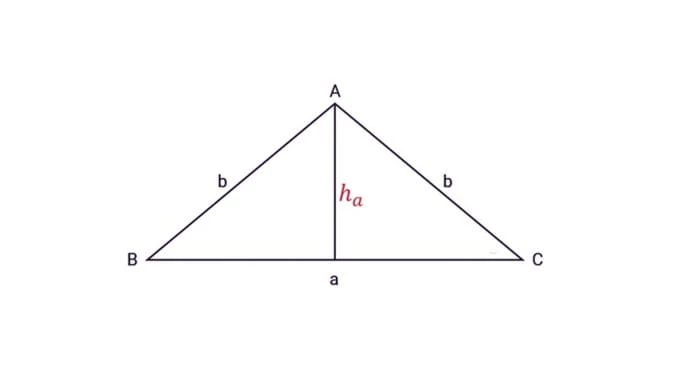
Khái niệm tam giác cân: “Tam giác cân là tam giác có 2 cạnh bằng nhau”. Đối với tam giác cân DEF, ta có công thức:

S = (a x h)/2

Trong đó:

• a là chiều dài cạnh.
• h là chiều cao của tam giác (đoạn thẳng hạ từ đỉnh xuống đáy).

Như vậy, diện tích tam giác cân bằng tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.

Bài tập ứng dụng:

Tính diện tích của tam giác cân DEF có độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm.

Giải: Diện tích của hình tam giác DEF là: S=(6 x 7): 2 = 6m2

2.3. Cách tính diện tích hình tam giác đều

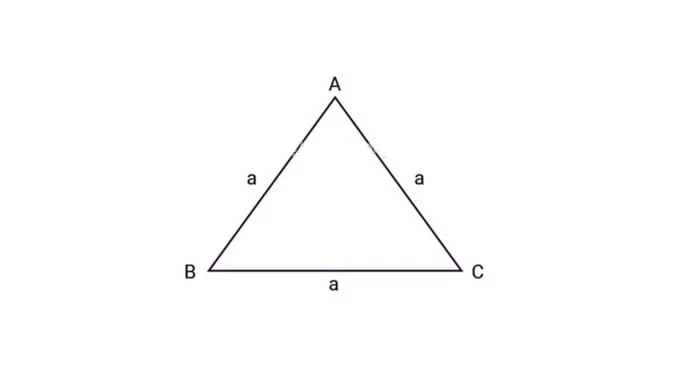
Khái niệm tam giác đều: “Tam giác đều là tam giác có 3 cạnh bằng nhau”. Cách tính diện tích tam giác đều cũng tương tự như tam giác thường: bằng tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.

S = (a x h)/2

Trong đó:

• a là chiều dài cạnh.
• h là chiều cao của tam giác (đoạn thẳng hạ từ đỉnh xuống đáy).

Bài tập ứng dụng:

Tính diện tích của tam giác đều XYZ có độ dài một cạnh tam giác bằng 6cm và đường cao bằng 10cm.

Giải: Diện tích hình tam giác XYZ là: S=(6 x 10) : 2 = 30 cm2

2.4. Cách tính diện tích hình tam giác vuông

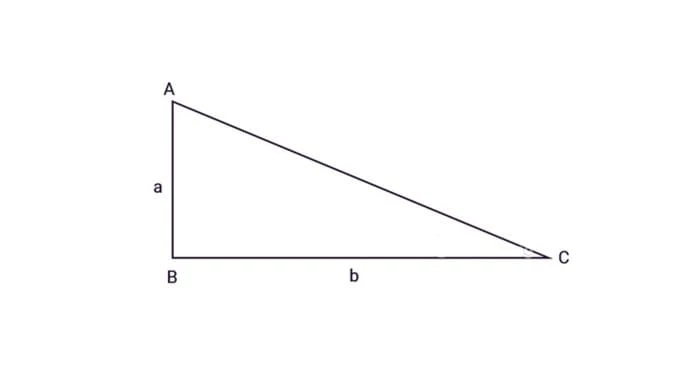
Tam giác vuông là tam giác có một góc bằng 90 độ. Cách tính diện tích tam giác vuông cũng tương từ: bằng ½ tích của đáy và chiều cao. Tuy nhiên vì chiều cao trong tam giác vuông ứng với một cách góc vuông nên suy ra: diện tích tam giác vuông bằng ½ tích hai cạnh góc vuông. Ta có công thức:

S = (a x b)/2

Trong đó a, b là độ dài hai cạnh góc vuông.

Bài tập ứng dụng:

Tính diện tích của tam giác vuông ABC có hai cạnh góc vuông lần lượt là 3cm và 4cm.

Giải: Diện tích của hình tam giác vuông ABC là: (3 x 4) : 2 = 6 cm2

2.5. Cách tính diện tích hình tam giác vuông cân

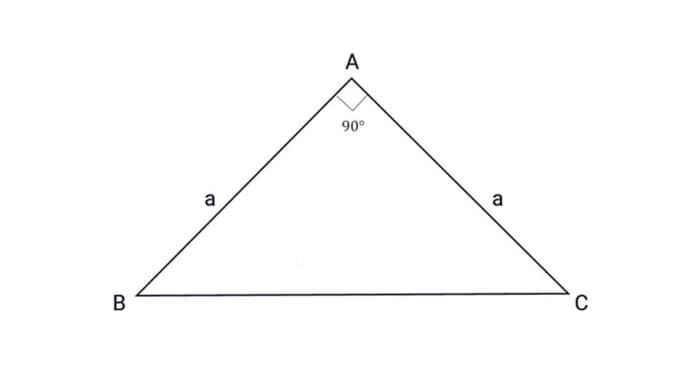
Tam giác vuông cân là tam giác có một góc bằng 90 độ và có chiều dài hai cạnh bên bằng nhau. Ta có công thức tính diện tích tam giác vuông cân:

S = ½  x a2 = ½ x a x a

Trong đó a là độ dài cạnh bên.

Bài tập ứng dụng:

Tính diện tích của tam giác vuông ABC có hai cạnh góc vuông đều bằng 4cm.

Giải: Diện tích tam giác vuông ABC là: ½ x 4 x 4 = 8 cm2

Như vậy, chung quy lại, cách tính diện tích tam giác lớp 5 là: ½ tích của của đáy và chiều cao. Tùy vào loại tam giác mà chiều cao có thể trùng với cạnh bên (như tam giác vuông và vuông cân). Tuy nhiên, ở cấp độ kiến thức lớp 5, bé chỉ cần nắm vững công thức trên là có thể giải được các bài toán diện tích hình tam giác.

3. Các dạng bài áp dụng cách tính diện tích hình tam giác lớp 5

Có nhiều dạng bài về tính diện tích hình tam giác, tùy vào mỗi cấp học mà sẽ có những dạng toán cần ứng dụng những cấp độ kiến thức khác nhau. Đối với cấp bậc kiến thức lớp 5, bé chỉ cần nắm vững các dạng toán sau:

Dạng 1: Tính diện tích tam giác khi biết độ dài cạnh đáy và chiều cao.

Dạng 2: Tính độ dài cạnh đáy khi biết diện tích tam giác và chiều cao.

Dạng 3: Tính chiều cao của tam giác khi biết diện tích tam giác và độ dài cạnh đáy.

Cách giải các dạng toán trên, cơ bản là dựa trên công thức S = ½ (a x h). Bài toán sẽ cung cấp dữ liệu của 2 trong 3 biến số, ta sẽ quy về dạng toán “tìm x” để tìm ra đáp án.

4. Làm thế nào để bé học nhanh cách tính diện tích hình tam giác lớp 5?

“Ôn luyện” là cách duy nhất giúp bé học nhanh, áp dụng nhuần nhuyễn cách tính diện tích hình tam giác lớp 5. Để giúp việc ôn luyện của bé không bị nhàm chán, cha mẹ và giáo viên nên xây dựng cho bé nền tảng kiến thức vững chắc về toán. Không nên ép bé học kiến thức cao hơn khi kiến thức nền của bé vẫn còn yếu.

Ngoài ra, nên tạo cho bé sự hứng thú qua việc áp dụng kiến thức vào đời sống thực tiễn. Chẳng hạn như, “đố” con tính được diện tích của các đồ vật có hình dạng tam giác trong nhà, ở trường,... Chỉ khi bé hiểu được sự hữu ích của cách tính diện tích hình tam giác thì bé mới cảm thấy hứng thú học kiến thức.

5. Kết luận

Vừa là tổng hợp những cách tính diện tích hình tam giác lớp 5. Đây thuộc dạng toán cơ bản trong hình học và khác khó đối với các bé lớp 5. Do vậy, trong quá trình hướng dẫn bé, chúng ta cần sự kiên nhẫn và cố gắng giải thích đơn giản.

Các bạn học sinh lớp 5 chắc cũng đang học đến bài cách rút gọn phân số. Do đó, đừng quên tham khảo thêm bài viết cực hay của BingGo Leaders nhé.