THUỘC LÒNG CÔNG THỨC TÍNH CHI VI HÌNH BÌNH HÀNH KÈM BÀI TẬP ÁP DỤNG

Hình học là một phần cực kỳ quan trọng trong kiến thức của bộ môn Toán học. Ở lứa tuổi tiểu học, các con bắt đầu làm quen với đặc điểm, nhận biết, cách tính chu vi và diện tích của hình.

Trong nội dung hôm nay, BingGo Leaders muốn đề cập đến hình bình hành, cụ thể là công thức tính chu vi hình bình hành và các bài tập áp dụng.

1. Hình bình hành là gì?

Trước khi bàn đến câu chuyện tính chu vi, chúng ta hãy cùng khái quát lại đôi nét về hình bình hành nào.

1.1. Về khái niệm

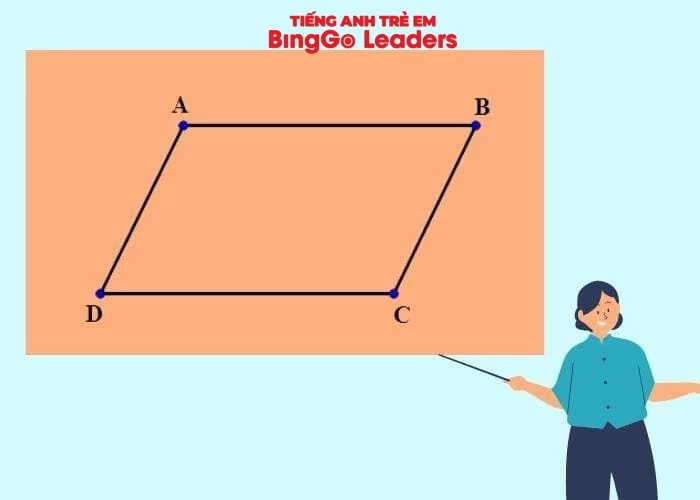
Hình bình hành là tứ giác đặc biệt, trong đó có 2 cặp cạnh đối song song hoặc vừa song song vừa bằng nhau. Có thể định nghĩa khái niệm hình bình hành là 1 dạng đặc biệt của hình thang.

1.2. Tính chất của hình bình hành

Một số tính chất của hình bình hành là: 

• Các cạnh đối bằng nhau: Ví dụ có hình bình hành ABCD (lần lượt là 4 đỉnh của hình), khi đó cạnh AB= CD và AD= BC.
• Các góc đối bằng nhau: Góc A=C và Góc B=D.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường: Gọi trung điểm của 2 đường chéo là O, khi đó AO=OC và BO=OD.

1.3. Dấu hiệu nhận biết hình bình hành

Nắm vững dấu hiệu nhận biết hình bình hành rất quan trọng, kiến thức này giúp ích trong việc vận dụng vào làm bài tập. Các con cần nắm rõ những dấu hiệu này để không nhầm lẫn hình bình hành với các hình khác. Cụ thể, cần ghi nhớ 2 dấu hiệu dưới đây:

• Hình bình hành là một dạng đặc biệt của tứ giác

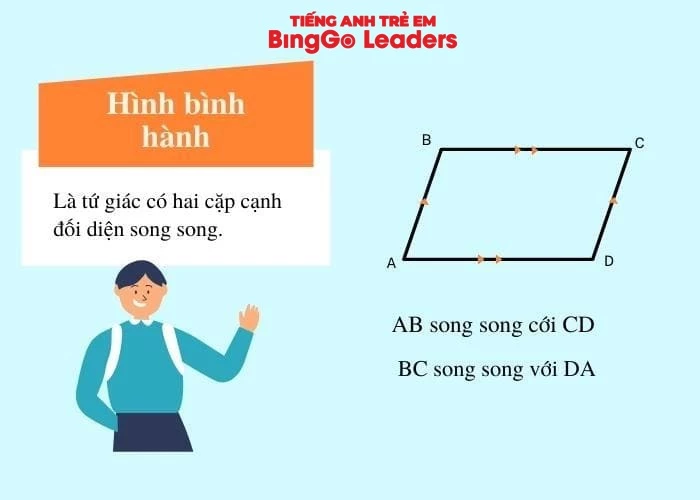
1- Tứ giác có cặp cạnh đối song song là hình bình hành

2 - Trong một tứ giác, nếu 1 trong 2 cặp cạnh đối bằng nhau là hình bình hành

3 - Trong từ giác, cặp cạnh đối vừa song song vừa bằng nhau là hình bình hành

4 - Trong một tứ giác, 2 góc đối bằng nhau là hình bình hành

5 - Hai đường chéo trong tứ giác giao nhau tại trung điểm mỗi đường là hình bình hành.

• Hình bình hành là hình thang đặc biệt

Trong hình thang có 2 cạnh đáy hoặc hai cạnh bên bằng nhau là hình bình hành

Ví dụ: Cho hình thang ABCD, trong đó AC = DC (hai cạnh đáy). Vậy hình thang ABCD là hình bình hành.

2. Công thức tính chu vi hình bình hành

Chu vi là đường bao quanh của bất cứ hình nào cần tính. Như vậy, công thức tính chu vi hình bình hành tổng chiều dài của 4 cạnh, nghĩa là cộng 4 cạnh lại lại với nhau. Hoặc tính chu vi bằng 2 lần tổng một cặp cạnh kề nhau.

Công thức cụ thể: 

P = 2 x (a+b)

Trong đó:

• P là ký hiệu chu vi hình bình hành
• a và b là hai cạnh của hình bình hành ABCD

3. Bài tập áp dụng công thức tính chu vi hình bình hành

Ghi nhớ công thức tính chu vi thôi mà chưa đủ. Các con hãy vận dụng ngay kiến thức mình vừa học được qua 3 bài tập nhỏ mới mức độ từ cơ bản đến nâng cao dưới đây nhé. 

3.1. Dạng 1 - Bài tập cơ bản

Dạng bài này không khó, con chỉ cần ghi nhớ công thức là có thể làm được.

Đề bài

Cho hình bình hành ABCD có chiều dài 2 cạnh liền kề lần lượt là a = 6cm và b= 3 cm. Yêu cầu: Tính chu vi hình bình hành ABCD?

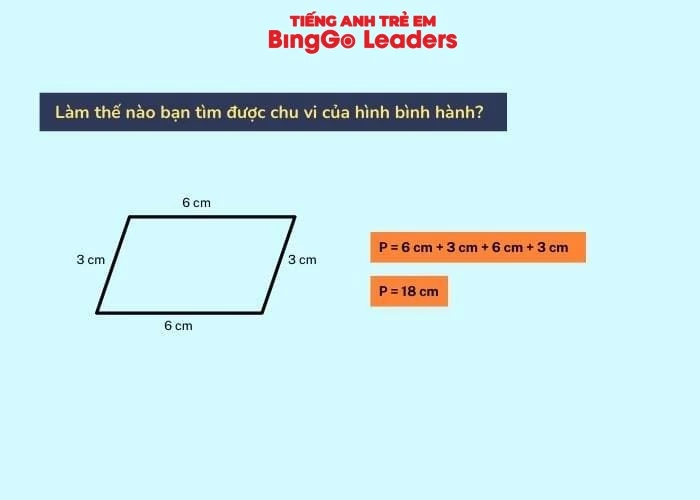
Hướng dẫn cách làm:

Ta có công thức tính chu vi hình bình hành là:

P = 2 x (a+b) 

Trong đó: a và b là 2 cạnh liền kề, a= 6 cm và b= 3 cm

Vậy P (ABCD) = 2 x (6+3) = 2 x 9 = 18 cm

3.2. Dạng 2 - Bài tập ngược

Đây là dạng bài tập cho sẵn chu vi của hình bình hành và một dữ kiện có liên quan. Yêu cầu tính nửa chu vi và tìm chiều dài các cạnh của hình bình hành.

Đề bài

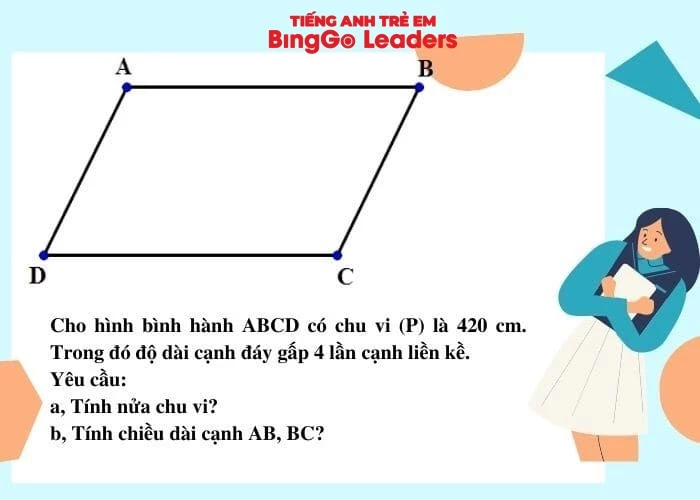
Hướng dẫn cách làm

a, Ta có chu vi hình bình hành ABCD = 420 cm (Theo dữ liệu đã cho)

Vậy nửa chu vi hình bình hành = P : 2 = 42 : 2 = 220 (cm)

b, Với hình thang ABCD thì AB, CD là cạnh đáy và BC, AD là cạnh bên.

Ta có công thức tính chu vi hình bình hành là:

P = 2 x (a+b)                          

Theo bài cho, ta có: độ dài cạnh đáy gấp 4 lần cạnh liền kề. 

+ Chiều dài cạnh bên là BC

BC = 220 : (4+1) = 44 (cm)

+ Chiều dài cạnh đáy của hình bình hành là: 44 x 4 = 176 (cm)

Vậy:

a, Nửa chu vi của hình bình hành ABCD là 220cm

b, Cạnh đáy của hình bình hành ABCD có chiều dài là 176cm, cạnh bên của hình bình hành có chiều dài là 44cm.

3.3. Dạng 3 - Bài tập quy đổi đơn vị tính

Bài tập quy đổi thường không có dạng cụ thể, thông thường là các dữ kiện cho liên quan đến nhau và ở nhiều đơn vị tính. Ví dụ như cm, dm, km… 

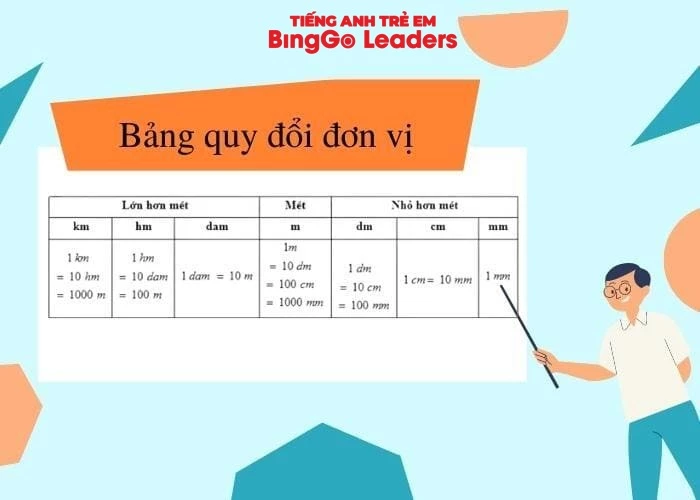
Theo đó để làm tốt dạng bài này, ba mẹ cùng bé ôn tập lại cách quy đổi một số đơn vị nhé. Cụ thể:

Km (Ki-lô-mét): 1km = 1000m

Dm (Đề-xi-mét): 1dm = 10cm.

Đề bài

Cho hình bình hành ABCD. Trong đó, độ dài cạnh đáy AB bằng a, độ dài cạnh bên BC bằng b. Yêu cầu tính chu vi biết rằng:

a) a = 40 cm; b = 33 cm.

b) a = 360 cm; b = 5,5 dm.

c) a = 1 km500m; b = 440m.

Hướng dẫn cách làm

Áp dụng công thức tính chu vi hình bình hành là:

 P= 2 x (a+b)

a) P (ABCD)= 2x (40+33)= 146 (cm).

Vậy: Chu vi hình bình hành ABCD là 146 cm.

b) Đổi 360 cm= 36 dm

P (ABCD)= 2 x (36+5,5)= 41,5 dm

Vậy: Chu vi hình bình hành ABCD là 41,5 dm.

c) Đổi 1km200m = 1500m.

P (ABCD)= 2 x (1500+440)= 39+880 (m).

Vậy: Chu vi hình bình hành ABCD là 3880 m.

Xem thêm: Cộng số đo thời gian toán lớp 5 - Lý thuyết kèm bài tập thực hành

4. Lời kết

Qua bài viết trên, các con đã hiểu rõ hơn và năm được những kiến thức cơ bản liên quan đến hình bình hành, đặc biệt là nhớ thuộc lòng công thức tính chu vi hình bình hành. 

Ngoài ra, ba mẹ có thể ghé ngay chuyên mục blog nuôi dạy con của BingGo Leaders để cập nhật thêm nhiều kiến thức thú vị trong việc nuôi dạy trẻ nhé.